勾股定理的证明方法_勾股定理的证明方法最简单的6种

勾股定理的证明方法_勾股定理的证明方法最简单的6种

       今天，我将与大家分享关于勾股定理的证明方法的最新动态，希望我的介绍能为有需要的朋友提供一些参考和建议。

1.十种方法证明勾股定理

2.勾股定理10种证明方法附图

3.勾股定理的证明方法 只需3步即可做出证明

4.勾股定理的多种证明方法

5.证明勾股定理的三种方法

十种方法证明勾股定理

       十种方法证明勾股定理有欧拉定理证明法、代数证明法、数学归纳法证明、相似三角形证明法、向量证明法、向量证明法、割圆术证明法、平面几何证明法、解析几何证明法、解析几何证明法、三角函数证明法、古希腊证明法。

       1、欧拉定理证明法。

       构造出一个直角三角形，把它的两条直角边对应的两个正方形放在真角三角形外面，另一条边对应的正方形放在直角三角形内部。再利用欧拉定理计算出三个正方形的面积，可以证明勾股定理。

       2、代数证明法。

       利用代数的平方公式，扭直角三角形的两条直C边平方相加，再把斜边平方，然后再将两者相减，得到一个等式，即可证明勾股定理。

       3、数学归纳法证明。

       用数学归纳法证明勾股定理，证明当n为正整数时，定理成立。

       4、相似三角形证明法。

       构造出相似的三角形，利用相似三角形，性质，可以推导出勾股定理。

       5、向量证明法。

       用向量的几何意义证明勾股定理，首先利用向量的长度和夹角的公式计算出向量的长度和夹角，再利用向量的点积公式计算出勾股定理中的各个变量，最后推导出勾股定理。

       6、割圆术证明法。

       利用割圆术将直角三角形对角线作为半径画圆，利用圆上弧角定理，可以得到勾股定理。

       7、平面几何证明法。

       用平面几何证明勾股定理，利用平面几何图形的形状和大小关系，推导出勾股定理。

       8、解析几何证明法。

       用解析几何证明勾股定理，利用平面直角坐标系，将三角形的三个点用坐标表示出来，推导出勾股定理。

       9、三角函数证明法。

       用三角函数证明勾股定理，利用三角函数的性质，将三角形分离出直角三角形和非直角三角形，再用三角函数计算出各个变量，推导出勾股定理。

       10、古希腊证明法。

       古希腊人对勾股定理有自己的证明方法。即利用几何图形的形状和大小，通过构造几何图形推导出勾股定理。

勾股定理10种证明方法附图

       证法1

        作四个全等的直角三角形,设它们的两条直角边长分别为a、b ,斜边长为c.把它们拼成如图那样的一个多边形,使D、E、F在一条直线上.过点C作AC的延长线交DF于点P.∵ D、E、F在一条直线上,且RtΔGEF ≌ RtΔEBD,∴ ∠EGF = ∠BED,∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180°―90°= 90° 又∵ AB = BE = EG = GA = c,∴ ABEG是一个边长为c的正方形.∴ ∠ABC + ∠CBE = 90° ∵ RtΔABC ≌ RtΔEBD,∴ ∠ABC = ∠EBD.∴ ∠EBD + ∠CBE = 90° 即 ∠CBD= 90° 又∵ ∠BDE = 90°,∠BCP = 90°,BC = BD = a.∴ BDPC是一个边长为a的正方形.同理,HPFG是一个边长为b的正方形.设多边形GHCBE的面积为S,则 a^2+b^2=c^2

        证法2

        作两个全等的直角三角形,设它们的两条直角边长分别为a、b（b>a） ,斜边长为c.再做一个边长为c的正方形.把它们拼成如图所示的多边形,使E、A、C三点在一条直线上.过点Q作QP‖BC,交AC于点P.过点B作BM⊥PQ,垂足为M；再过点 F作FN⊥PQ,垂足为N.∵ ∠BCA = 90°,QP‖BC,∴ ∠MPC = 90°,∵ BM⊥PQ,∴ ∠BMP = 90°,∴ BCPM是一个矩形,即∠MBC = 90°.∵ ∠QBM + ∠MBA = ∠QBA = 90°,∠ABC + ∠MBA = ∠MBC = 90°,∴ ∠QBM = ∠ABC,又∵ ∠BMP = 90°,∠BCA = 90°,BQ = BA = c,∴ RtΔBMQ ≌ RtΔBCA.同理可证RtΔQNF ≌ RtΔAEF.即a^2+b^2=c^2

        证法3

        作两个全等的直角三角形,设它们的两条直角边长分别为a、b（b>a） ,斜边长为c.再作一个边长为c的正方形.把它们拼成如图所示的多边形.分别以CF,AE为边长做正方形FCJI和AEIG,∵EF=DF-DE=b-a,EI=b,∴FI=a,∴G,I,J在同一直线上,∵CJ=CF=a,CB=CD=c,∠CJB = ∠CFD = 90°,∴RtΔCJB ≌ RtΔCFD ,同理,RtΔABG ≌ RtΔADE,∴RtΔCJB ≌ RtΔCFD ≌ RtΔABG ≌ RtΔADE ∴∠ABG = ∠BCJ,∵∠BCJ +∠CBJ= 90°,∴∠ABG +∠CBJ= 90°,∵∠ABC= 90°,∴G,B,I,J在同一直线上,a^2+b^2=c^2

        证法4

        作三个边长分别为a、b、c的三角形,把它们拼成如图所示形状,使H、C、B三点在一条直线上,连结 BF、CD.过C作CL⊥DE,交AB于点M,交DE于点L.∵ AF = AC,AB = AD,∠FAB = ∠GAD,∴ ΔFAB ≌ ΔGAD,∵ ΔFAB的面积等于,ΔGAD的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM的面积 =.同理可证,矩形MLEB的面积 =.∵ 正方形ADEB的面积 = 矩形ADLM的面积 + 矩形MLEB的面积 ∴ 即a^2+b^2=c^2

勾股定理的证明方法 只需3步即可做出证明

       勾股定理10种证明方法附图的回答如下：

       勾股定理是数学中一个非常重要的定理，它揭示了直角三角形三条边的数量关系。

下面给出10种证明勾股定理的方法，并附带有说明。

毕达哥拉斯证明法

       这是勾股定理的最早证明之一，由古希腊数学家毕达哥拉斯给出。证明的方法是通过构造一个直角三角形，并利用三角形的面积公式来证明。

欧几里得证明法

       欧几里得是古希腊数学家，他的《几何原本》是世界上最早的公理化数学著作。在书中，欧几里得给出了勾股定理的一个简单证明。

邹元治证明法

       这是中国清代数学家邹元治的一种证明方法。他利用了三角形面积的另一种计算方法来证明勾股定理。

帕斯卡证明法

       帕斯卡是法国数学家和物理学家，他通过巧妙地利用三角形面积公式，证明了勾股定理。

雷登证明法

       雷登是荷兰数学家，他利用了三角形的相似性质来证明勾股定理。

普鲁士夫证明法

       普鲁士夫是捷克数学家，他通过构造一个直角三角形，并利用三角形的面积公式来证明勾股定理。

阿尔辛证明法

       阿尔辛是土耳其数学家，他利用了三角形的内角和性质来证明勾股定理。

哈格森证明法

       哈格森是瑞士数学家，他通过构造一系列等腰直角三角形来证明勾股定理。

牛顿证明法

       牛顿是英国数学家和物理学家，他通过微积分的方法证明了勾股定理。

皮克特证明法

       皮克特是美国数学家，他利用了三角形的边长和角度之间的关系来证明勾股定理。

总结：

       以上10种证明方法分别从不同的角度和思路出发，证明了勾股定理的正确性。其中，直接证明法和逆定理证明法是最常用的方法之一，而其他方法则可以拓展我们的思路和视野，加深对勾股定理的理解和应用。

       无论采用哪种方法，都需要我们在理解定理的基础上，灵活运用相关的数学知识进行推导和计算。

勾股定理的多种证明方法

       勾股定理的证明方法如下：

        1、以a b为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于2分之一ab。

        2、AEB三点在一条直线上，BFC三点在一条直线上，CGD三点在一条直线上。

        3、证明四边形EFGH是一个边长为c的正方形后即可推出勾股定理。

证明勾股定理的三种方法

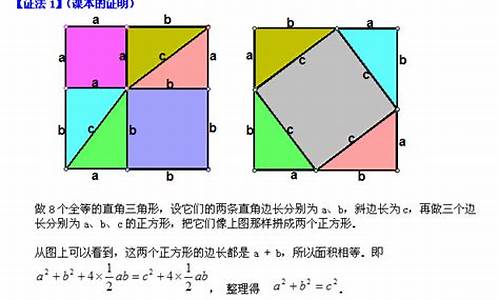
       毕达哥拉斯证法：

       一、传说中毕达哥拉斯的证法（图1）

左边的正方形是由1个边长为的正方形和1个边长为的正方形以及4个直角边分别为a、b，斜边为c的直角三角形拼成的。右边的正方形是由1个边长为的正方形和4个直角边分别为a、b，斜边c为的直角三角形拼成的。因为这两个正方形的面积相等(边长都是a+b)，所以可以列出等式a?+b?+4×1/2ab=c?+4×1/2ab，化简得a?+b?=c?。

在西方，人们认为是毕达哥拉斯最早发现并证明这一定理的，但遗憾的是，他的证明方法已经失传，这是传说中的证明方法，这种证明方法简单、直观、易懂。

       二、赵爽弦图的证法

       第一种方法：边长为的正方形可以看作是由4个直角边分别为a、b，斜边为c 的直角三角形围在外面形成的。因为边长为的正方形面积加上4个直角三角形的面积等于外围正方形的面积，所以可以列出等式c?+4×1/2ab=（a+b)?，化简得a?+b?=c?。

第二种方法：边长为的正方形可以看作是由4个直角边分别为a、b，斜边为 c的直角三角形拼接形成的（虚线表示），不过中间缺出一个边长为（b-a)的正方形“小洞”。

因为边长为c的正方形面积等于4个直角三角形的面积加上正方形“小洞”的面积，所以可以列出等式c?=(b-a)?+4×1/2ab，化简得a?+b?=c?。

这种证明方法很简明，很直观，它表现了我国古代数学家赵爽高超的证题思想和对数学的钻研精神，是我们中华民族的骄傲。

       三、美国第20任总统茄菲尔德的证法

       这个直角梯形是由2个直角边分别为a、b，斜边为c 的直角三角形和1个直角边为c

的等腰直角三角形拼成的。因为3个直角三角形的面积之和等于梯形的面积，所以可以列出等式c?/2+2×1/2ab=(b+a)(a+b)/2，化简得a?+b?=c?。

这种证明方法由于用了梯形面积公式和三角形面积公式，从而使证明更加简洁，它在数学史上被传为佳话。

       勾股定理：勾股定理是一个基本的几何定理，在中国，《周髀算经》记载了勾股定理的公式与证明，相传是在商代由商高发现，故又有称之为商高定理；三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释，又给出了另外一个证明。直角三角形两直角边（即“勾”，“股”）边长平方和等于斜边（即“弦”）边长的平方。也就是说，设直角三角形两直角边为a和b，斜边为c，那么a?+b?=c?。勾股定理现发现约有400种证明方法，是数学定理中证明方法最多的定理之一。勾股数是组成a?+b?=c?的正整数组(a,b,c)。(3,4,5)就是勾股数。?目前初二学生教材的证明方法采用赵爽弦图，证明使用青朱出入图。勾股定理是一个基本的几何定理，它是用代数思想解决几何问题的最重要的工具之一，是数形结合的纽带之一。直角三角形两直角边的平方和等于斜边的平方。如果用a、b和c分别表示直角三角形的两直角边和斜边，那么a?+b?=c?。

       证明勾股定理的方法：

1、正方形面积法

       这是一种很常见的证明方法，具体使用的是面积来证明的。以三角形的三边分别作三个正方形，发现两个较小的正方形面积之和等于较大的那个三角形。勾股定理得到证明。

2、赵爽弦图

       赵爽弦图是指用四个斜边长为c，较长直角边为a,较短直角边为c的指教三角形组成一个正方形。在这个较大的正方形里还有一个较小的正方形。通过计算整体的面积算出勾股定理。

3、梯形证明法

       梯形证明法也是一种很好的证明方法。即选两个一样的直角三角形一个横放，一个竖放，将高处的两个点相连。计算梯形的面积等于三个三角形的面积分别相加，从而证明勾股定理。

4、青出朱入图

       青出朱入图是我国古代数学家刘徽提出的一种证明勾股定理的方法，是使用割补的方法进行的。就是将两个大小不等的正方形边长分别为a,b,然后通过割补的方法将它们拼成一个较大的正方形。

5、毕达哥拉斯证明

       毕达哥拉斯的证明方法，也是证明面积相等，蛋是才去的方法是对三角形进行了移动。比如将原来的四个分散在四周的三角形，两两相组合，发现两个正方形的面积和两个长方形的面积相等。

6、三角形相似证明

       利用三角形的相似性来证明勾股定理。就是将三角形从直角边作垂线，这单个三角形相似。以三边分别作正方形，因为边成比例，所以面积也具有成比例的关系。

勾股定理

       勾股定理，是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

       勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。

       在中国，周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派，他们用演绎法证明了直角三角形斜边平方等于两直角边平方之和。

       好了，今天我们就此结束对“勾股定理的证明方法”的讲解。希望您已经对这个主题有了更深入的认识和理解。如果您有任何问题或需要进一步的信息，请随时告诉我，我将竭诚为您服务。